Saturday, February 28, 2009
Recognizing/printing real numbers in real time
In the first blog post for the course, on the history of complexity, I saw mention of the question of whether the number $\sqrt{2}$ could be printed out by a Turing Machine at a rate of $O(1)$ time per digit. I had never heard of the problem before. Apparently one can ask similar questions about recognizing in "real time" whether a number is, say, $\sqrt{2}$; for more, see this post on Dick Lipton's blog.
Thursday, February 26, 2009
Lecture 13
Today we covered: Parity has unbounded fan-in circuits of depth-$d$ size-$2^{\Theta(n^{1/(d-1)})}$. Hastad's Theorem statement: This is also a lower bound for constant $d$. Proof in the case $d = 2$ (CNF, DNF). Razborov-Smolensky proof with $1/(4d)$ rather than $1/(d-1)$. Its main tool: For any $k$, $\epsilon$, there is a probability distribution on $k$-variable polynomials of degree $O(\log k \log(1/\epsilon))$ such that for every $k$-bit input $x$ we have $\Pr[p(x) = OR(x)] \geq 1 - \epsilon$ when $p$ is chosen from the distribution. Expanding functions $f : \{-1,1\}^n \to \mathbb{R}$ in the Fourier basis.
Wednesday, February 25, 2009
Homework 2 wrapup
By the way: #4 is a theorem of Krentel; the class in #5 is actually called $S_2P$ (not $S$) and the problem is a theorem of Cai; #6 is a theorem of Mulmuley-Valiant-Vazirani.
Tuesday, February 24, 2009
Lecture 12
Today we covered: Definitions of $AM[k]$ and $MA[k]$; $AM[k]$ and $MA[k]$ unchanged if perfect completeness required (statement); $MA = MA[2] \subseteq AM[2] = AM$; $AM[k] = AM[2]$ for all constant $k$; indeed, $AM[4r] \subseteq AM[2r+1]$ for any $r = r(n)$; $AM \subseteq \Pi_2$; Boppana-Hastad-Zachos Theorem, $coNP \subseteq AM \Rightarrow PH = AM$; Graph-Non-Isomorphism is not $NP$-complete unless the hierarchy collapses to $\Simga_2$; Goldwasser-Sipser Theorem, $k$-round private-coin interactive proofs are doable with $(k+10)$-round public-coin interactive proofs, hence $AM$ is unchanged if public coins are required; set size lower bound protocol in public coins $AM$.
Solutions to Homework 2
I will be returning Homework 2 in class today. The class average on this homework is 79%. Solutions for the homework will once again be available upon request; please email me if you would like a copy.
Saturday, February 21, 2009
Derandomization of space classes
Understanding the exact computational power of randomness is an intriguing and very challenging problem in computer science. Although we are far away from an answer, a lot of nice results have emerged in the last two decades, particularly in the area of space bounded computations. In this post, we will look at a couple of such results. We will restrict our attention to randomized log-space machines, or the complexity class BPL, but the results we mentioned generalize to BSPACE($s(n)$) for any space constructible function $s(n) \ge \log n$. Recall that a BPL machine M
for a language L is a randomized machine running in log-space and satisfying the following conditions:
$x \in$ L $\Rightarrow$ Pr[M accepts $x$] $\ge \frac{2}{3}$
$x \notin$ L $\Rightarrow$ Pr[M accepts $x$] $\le \frac{1}{3}$
Also we know that, the computation of such a machine on input $x$ can be seen as a random walk on a graph $G$, called the ``configuration graph''. Each node in this graph represents a configuration of the machine and each edge represents a valid transition. Let us denote by $d$, the total number of nodes in this graph and let us assume that that the graph has a unique start state $c_{start}$ and unique accept and reject states $c_{accept}$ and $c_{reject}$. Since, the machine runs in log-space we know that $d$ is polynomial in the length of the input. We can also associate, with this graph, a matrix Q called the ``transition matrix''. The entry Q[i,j] in this matrix contains the probability that the machine M goes from configuration $i$ to configuration $j$ in one step. This way of looking at a BPL machine is very convenient since now simulating the machine is equivalent to computing the $p$ step transition probability $Q^p$[$c_{start}$ , $c_{accept}$], for any $p \ge d$. If this probability is more than $\frac{2}{3}$ we accept. If this probability is less than $\frac{1}{3}$, we reject. Savitch's idea of repeated matrix squaring computes this probability exactly giving us the following derandomization result $ BPL \subseteq L^2$. We would also be interested in the running time used by these simulations, hence we will rewrite the above result as BPL $\subseteq$ DTISP($n^{O(\log n)}$,$(\log n)^2$).
Further improvements to this result are all based on a very nice ``duality'' between hardness and randomness. This relationship was made concrete in a paper by Noam Nisan and Avi Wigderson. The high level idea is as follows: Suppose we have pseudo-random generator which takes as input a
short truly random seed and can produce a very long sequence of bits which look random to any probabilistic machine. We can then use these pseudo-random bits instead of truly random bits to simulate the machine thereby reducing the amount of randomness used. This in turn has the potential to lead to better deterministic simulations. Unfortunately, pseudo-random generators are known to exist only under the assumption that certain cryptographic objects called one way functions exist. However, it is possible to construct specialized unconditional pseudo-random
generators which can fool a particular class of machines C. Here is one way to do it, choose a class of functions, one for each input length, which is hard for the class C. In other words for every $n \ge 1$, for every machine M $ \in$ C, we must have |$Pr_{x \in U_n}$[M($x$) = f($x$)] $-$ $\frac{1}{2}$| $ \le \epsilon$, where $U_n$ is uniform distribution over $\{0,1\}^n$ and $\epsilon $ is very small(lets say $\frac{1}{n^2}$). What this means is that any machine in C can not do much better then random guessing when asked to predict the values of the hard functions. If we have such a class of functions, then here is a very simple pseudo-random generator which stretches its seed by 1 bit: $G_f : s \mapsto (s,f(s))$. Notice, that although we are only appending $f(s)$ at the end, no machine in C can distinguish that from a truly random bit with significant probability. This was roughly the idea behind the pseudo-random generator proposed by Nisan and Wigderson.
Later, in a breakthrough result, Noam Nisan gave a pseudo-random generator which can fool all probabilistic log-space machines and uses only $(\log n)^2$ bits of randomness. Notice, that this is an exponential improvement since a BPL machine can potentially use poly($n$) random bits, where $n$ is the length of the input. Virtually, every result in derandomizing space complexity classes has used some ideas from Nisan's paper. Before stating Nisan's result some definitions:
Definition 1:
For a vector $x \in {\Re}^d$, we define the $L_1$ norm of $x$ to be ||$x$|| = $\sum_i x_i$. For a $d \times d$ matrix over $\Re$, we define the norm of M, ||M||, to be the maximum over all the rows M[$i$,.] of ||M[$i$,.]||.
Definition 2:
If M and N are square matrices of the same dimension and $a$ is a positive real number, we say that M approximates N with accuracy a if ||M $-$ N|| $ \le 2^{-a}$.
Recall that simulating a BPL machine is equivalent to calculating the matrix $Q^p$, for some $p \ge d$. Hence, we now state and view Nisan's result as as randomized algorithm for approximating this matrix. We will call Nisan's algorithm PRS which stands for pseudorandom repeated squaring.
Theorem:
Let $a$ be an integer. Given as input a $d \times d$ transition matrix Q and an integer $r$, the PRS algorithm takes a random string $h$ of size $O(r(\log n))$ as input, runs in space $O(r + \log n)$ and computes another matrix $Q^\prime$, such that $Q^\prime$ approximates $Q^{2^{r}}$ with accuracy $a$ and error probability $2^{-2a}$.
Notice, that it is enough to approximate the entries in the matrix $Q^{2^r}$, since we only want to detect a significant gap in the acceptance probability of $\frac{2}{3}$ when $x \in $ L and the probability of $\frac{1}{3}$, when $x \notin$ L. For simulating BPL, we need to choose $r$ such that $2^r \ge d$. Choosing $r = O(\log n)$, gives us the desired log-space simulation which uses $O((\log n)^2)$ bits of randomness. A straightforward derandomization of this algorithm, i.e. enumerating through all the possible choices of the random seed, will not help us improve on the bound given by Savitch's theorem(WHY?). But, in a later paper Nisan observed that most of the bits in the random seed can actually be calculated deterministically, reducing the randomness used by the algorithm to $O(\log n)$. Derandomizing this new algorithm gives a deterministic simulation of BPL which uses $O((\log n)^2)$ space and $n^{O(1)}$ time! Hence, Nisan was able to show that BPL $\subseteq$ DTISP($n^{O(1)}$,$(\log n)^2$). In other words, Nisan showed that BPL $\subseteq SC$(``Steve's'' class). In a later work Nisan, Endre Szemer$\grave{\textrm{e}}$di, and Wigderson, in 1992, showed that undirected s-t connectivity(USTCONN) is in $L^{\frac{3}{2}}$. Of course, from Omar Reingold's result in 2004, we now know that USTCONN $\in$ L. But at that point the USTCONN $\in$ $L^{\frac{3}{2}}$ was a major indication that may be deterministic simulation of BPL could be done in $L^{\frac{3}{2}}$. This was achieved by Michael Saks and Shiyu Zhou and will be the last result covered in this post.
The main idea behind Saks and Zhou's result is to somehow balance the space usage and the randomness usage of the PRS algorithm. One way to do this is to try and combine Savitch's theorem and Nisan's PRS algorithm, i.e. try to do repeated matrix squaring but at each level of recursion, instead of calculating the matrix exactly, approximate it using the PRS algorithm. Lets see how it works in detail.
Consider the PRS algorithm again. Lets divide the input $r$ into two parts $r_1$ and $r_2$ such that $r = r_1r_2$. We can calculate $Q^{2^r}$ as a sequence matrices $Q_0$,$Q_1$,$\ldots$,$Q_{r_2}$, such that $Q_0$ = $Q^{2^{r_1}}$, $Q_{i+1}$ = ${Q_i}^{2^{r_1}}$ and $Q_{r_2}$ = $Q^{2^r}$. At each of the $r_2$ levels of the recursion we can use the PRS algorithm
to approximately calculate the matrices. We are going to use $O(\log n)$ space at each level for a total of $O(r_2 \log n)$ space. Also we are going to use $O(r_1 \log n)$ bits of randomness at each level for a total of $O(r \log n)$ bits of randomness. At present this does not seem very impressive, but what Saks and Zhou show is that we can actually use the same seed for the PRS algorithm at each level of recursion. This reduces the randomness complexity to $O(r_1 \log n)$. The reason why we can do that is the following: The analysis of the PRS algorithm shows that most of the seeds are good for a given fixed matrix. Hence, by union bound we must be able to show that most of the seeds are also good for a fixed set of matrices. If we can do that then we can set $r = O(\log n)$, and $r_1=r_2$, to get an algorithm with space complexity $O({(\log n }^{\frac{3}{2}})$ and randomness complexity $O({(\log n)}^{\frac{3}{2}})$. Then, a straightforward derandomization will give us the desired result that BPL $\subseteq L^{\frac{3}{2}}$. But there is a catch.
Notice that we cannot really apply the union bound argument to the matrices produced by the PRS algorithm since each of them depends on the seed used in the previous level of recursion. Saks and Zhou get around this problem by introducing the idea of random perturbations. The main observation is that we can apply the union bound argument to the sequence of matrices if they are not approximately calculated but exactly calculated as in Savitch's theorem. Now, the PRS algorithm guarantees that the matrices will be very close to the exact ones. Hence, if we just truncate the values in the matrices ignoring the lower order bits, we should be done. Except that we might have some bad roundings at boundary cases. Hence, what Saks and Zhou do is that they reduce the value of each entry in the matrix at each level by some random quantity and then truncate the values. In this way, the new matrices are independent of the seed used and we can then say that most of the seeds will be good for all these matrices. For random perturbations we increase the space usage at each level by $O(\log n)$. But the final space usage still is $O((\log n)^{\frac{3}{2}})$. That's it, we can now state Saks and Zhou's result that
$ BPL \subseteq DTISP(n^{O({(\log n)}^{.5})},{(\log n)}^{1.5}) $
Some follow-up work has been done after Saks and Zhou's result. For example, Jin-Yi Cai, Venkatesan Chakaravarthy and Dieter Van Melkebeek give a time-space tradeoff version of Saks and Zhou which says that, for any rational number $0 \le \alpha \le .5$, BPL $\subseteq$ DTISP($n^{O({(\log n)}^{.5-\alpha})}$,${(\log n)}^{1.5 + \alpha}$). Since then, Reingold's log-space algorithm for USTCONN has been a major result.
There is a general feeling in the community that we might be close to proving RL$=$L. In fact, Omar Reingold, Luca Trevisan and Salil Vadhan, in a paper in 2005, gave some strong evidence in favor of this.
Aside:
If you have read so far then a natural question to ask is: What about derandomization of time complexity classes. Can similar ideas be applied. Conceptually, Yes. Nisan's idea is pretty neat and generic. I have not done much survey but some initial reading seems to suggest that it is difficult to give unconditional pseudorandom generators which can fool time bounded complexity classes. May be the instructors can shed more light on this issue.
for a language L is a randomized machine running in log-space and satisfying the following conditions:
$x \in$ L $\Rightarrow$ Pr[M accepts $x$] $\ge \frac{2}{3}$
$x \notin$ L $\Rightarrow$ Pr[M accepts $x$] $\le \frac{1}{3}$
Also we know that, the computation of such a machine on input $x$ can be seen as a random walk on a graph $G$, called the ``configuration graph''. Each node in this graph represents a configuration of the machine and each edge represents a valid transition. Let us denote by $d$, the total number of nodes in this graph and let us assume that that the graph has a unique start state $c_{start}$ and unique accept and reject states $c_{accept}$ and $c_{reject}$. Since, the machine runs in log-space we know that $d$ is polynomial in the length of the input. We can also associate, with this graph, a matrix Q called the ``transition matrix''. The entry Q[i,j] in this matrix contains the probability that the machine M goes from configuration $i$ to configuration $j$ in one step. This way of looking at a BPL machine is very convenient since now simulating the machine is equivalent to computing the $p$ step transition probability $Q^p$[$c_{start}$ , $c_{accept}$], for any $p \ge d$. If this probability is more than $\frac{2}{3}$ we accept. If this probability is less than $\frac{1}{3}$, we reject. Savitch's idea of repeated matrix squaring computes this probability exactly giving us the following derandomization result $ BPL \subseteq L^2$. We would also be interested in the running time used by these simulations, hence we will rewrite the above result as BPL $\subseteq$ DTISP($n^{O(\log n)}$,$(\log n)^2$).
Further improvements to this result are all based on a very nice ``duality'' between hardness and randomness. This relationship was made concrete in a paper by Noam Nisan and Avi Wigderson. The high level idea is as follows: Suppose we have pseudo-random generator which takes as input a
short truly random seed and can produce a very long sequence of bits which look random to any probabilistic machine. We can then use these pseudo-random bits instead of truly random bits to simulate the machine thereby reducing the amount of randomness used. This in turn has the potential to lead to better deterministic simulations. Unfortunately, pseudo-random generators are known to exist only under the assumption that certain cryptographic objects called one way functions exist. However, it is possible to construct specialized unconditional pseudo-random
generators which can fool a particular class of machines C. Here is one way to do it, choose a class of functions, one for each input length, which is hard for the class C. In other words for every $n \ge 1$, for every machine M $ \in$ C, we must have |$Pr_{x \in U_n}$[M($x$) = f($x$)] $-$ $\frac{1}{2}$| $ \le \epsilon$, where $U_n$ is uniform distribution over $\{0,1\}^n$ and $\epsilon $ is very small(lets say $\frac{1}{n^2}$). What this means is that any machine in C can not do much better then random guessing when asked to predict the values of the hard functions. If we have such a class of functions, then here is a very simple pseudo-random generator which stretches its seed by 1 bit: $G_f : s \mapsto (s,f(s))$. Notice, that although we are only appending $f(s)$ at the end, no machine in C can distinguish that from a truly random bit with significant probability. This was roughly the idea behind the pseudo-random generator proposed by Nisan and Wigderson.
Later, in a breakthrough result, Noam Nisan gave a pseudo-random generator which can fool all probabilistic log-space machines and uses only $(\log n)^2$ bits of randomness. Notice, that this is an exponential improvement since a BPL machine can potentially use poly($n$) random bits, where $n$ is the length of the input. Virtually, every result in derandomizing space complexity classes has used some ideas from Nisan's paper. Before stating Nisan's result some definitions:
Definition 1:
For a vector $x \in {\Re}^d$, we define the $L_1$ norm of $x$ to be ||$x$|| = $\sum_i x_i$. For a $d \times d$ matrix over $\Re$, we define the norm of M, ||M||, to be the maximum over all the rows M[$i$,.] of ||M[$i$,.]||.
Definition 2:
If M and N are square matrices of the same dimension and $a$ is a positive real number, we say that M approximates N with accuracy a if ||M $-$ N|| $ \le 2^{-a}$.
Recall that simulating a BPL machine is equivalent to calculating the matrix $Q^p$, for some $p \ge d$. Hence, we now state and view Nisan's result as as randomized algorithm for approximating this matrix. We will call Nisan's algorithm PRS which stands for pseudorandom repeated squaring.
Theorem:
Let $a$ be an integer. Given as input a $d \times d$ transition matrix Q and an integer $r$, the PRS algorithm takes a random string $h$ of size $O(r(\log n))$ as input, runs in space $O(r + \log n)$ and computes another matrix $Q^\prime$, such that $Q^\prime$ approximates $Q^{2^{r}}$ with accuracy $a$ and error probability $2^{-2a}$.
Notice, that it is enough to approximate the entries in the matrix $Q^{2^r}$, since we only want to detect a significant gap in the acceptance probability of $\frac{2}{3}$ when $x \in $ L and the probability of $\frac{1}{3}$, when $x \notin$ L. For simulating BPL, we need to choose $r$ such that $2^r \ge d$. Choosing $r = O(\log n)$, gives us the desired log-space simulation which uses $O((\log n)^2)$ bits of randomness. A straightforward derandomization of this algorithm, i.e. enumerating through all the possible choices of the random seed, will not help us improve on the bound given by Savitch's theorem(WHY?). But, in a later paper Nisan observed that most of the bits in the random seed can actually be calculated deterministically, reducing the randomness used by the algorithm to $O(\log n)$. Derandomizing this new algorithm gives a deterministic simulation of BPL which uses $O((\log n)^2)$ space and $n^{O(1)}$ time! Hence, Nisan was able to show that BPL $\subseteq$ DTISP($n^{O(1)}$,$(\log n)^2$). In other words, Nisan showed that BPL $\subseteq SC$(``Steve's'' class). In a later work Nisan, Endre Szemer$\grave{\textrm{e}}$di, and Wigderson, in 1992, showed that undirected s-t connectivity(USTCONN) is in $L^{\frac{3}{2}}$. Of course, from Omar Reingold's result in 2004, we now know that USTCONN $\in$ L. But at that point the USTCONN $\in$ $L^{\frac{3}{2}}$ was a major indication that may be deterministic simulation of BPL could be done in $L^{\frac{3}{2}}$. This was achieved by Michael Saks and Shiyu Zhou and will be the last result covered in this post.
The main idea behind Saks and Zhou's result is to somehow balance the space usage and the randomness usage of the PRS algorithm. One way to do this is to try and combine Savitch's theorem and Nisan's PRS algorithm, i.e. try to do repeated matrix squaring but at each level of recursion, instead of calculating the matrix exactly, approximate it using the PRS algorithm. Lets see how it works in detail.
Consider the PRS algorithm again. Lets divide the input $r$ into two parts $r_1$ and $r_2$ such that $r = r_1r_2$. We can calculate $Q^{2^r}$ as a sequence matrices $Q_0$,$Q_1$,$\ldots$,$Q_{r_2}$, such that $Q_0$ = $Q^{2^{r_1}}$, $Q_{i+1}$ = ${Q_i}^{2^{r_1}}$ and $Q_{r_2}$ = $Q^{2^r}$. At each of the $r_2$ levels of the recursion we can use the PRS algorithm
to approximately calculate the matrices. We are going to use $O(\log n)$ space at each level for a total of $O(r_2 \log n)$ space. Also we are going to use $O(r_1 \log n)$ bits of randomness at each level for a total of $O(r \log n)$ bits of randomness. At present this does not seem very impressive, but what Saks and Zhou show is that we can actually use the same seed for the PRS algorithm at each level of recursion. This reduces the randomness complexity to $O(r_1 \log n)$. The reason why we can do that is the following: The analysis of the PRS algorithm shows that most of the seeds are good for a given fixed matrix. Hence, by union bound we must be able to show that most of the seeds are also good for a fixed set of matrices. If we can do that then we can set $r = O(\log n)$, and $r_1=r_2$, to get an algorithm with space complexity $O({(\log n }^{\frac{3}{2}})$ and randomness complexity $O({(\log n)}^{\frac{3}{2}})$. Then, a straightforward derandomization will give us the desired result that BPL $\subseteq L^{\frac{3}{2}}$. But there is a catch.
Notice that we cannot really apply the union bound argument to the matrices produced by the PRS algorithm since each of them depends on the seed used in the previous level of recursion. Saks and Zhou get around this problem by introducing the idea of random perturbations. The main observation is that we can apply the union bound argument to the sequence of matrices if they are not approximately calculated but exactly calculated as in Savitch's theorem. Now, the PRS algorithm guarantees that the matrices will be very close to the exact ones. Hence, if we just truncate the values in the matrices ignoring the lower order bits, we should be done. Except that we might have some bad roundings at boundary cases. Hence, what Saks and Zhou do is that they reduce the value of each entry in the matrix at each level by some random quantity and then truncate the values. In this way, the new matrices are independent of the seed used and we can then say that most of the seeds will be good for all these matrices. For random perturbations we increase the space usage at each level by $O(\log n)$. But the final space usage still is $O((\log n)^{\frac{3}{2}})$. That's it, we can now state Saks and Zhou's result that
$ BPL \subseteq DTISP(n^{O({(\log n)}^{.5})},{(\log n)}^{1.5}) $
Some follow-up work has been done after Saks and Zhou's result. For example, Jin-Yi Cai, Venkatesan Chakaravarthy and Dieter Van Melkebeek give a time-space tradeoff version of Saks and Zhou which says that, for any rational number $0 \le \alpha \le .5$, BPL $\subseteq$ DTISP($n^{O({(\log n)}^{.5-\alpha})}$,${(\log n)}^{1.5 + \alpha}$). Since then, Reingold's log-space algorithm for USTCONN has been a major result.
There is a general feeling in the community that we might be close to proving RL$=$L. In fact, Omar Reingold, Luca Trevisan and Salil Vadhan, in a paper in 2005, gave some strong evidence in favor of this.
Aside:
If you have read so far then a natural question to ask is: What about derandomization of time complexity classes. Can similar ideas be applied. Conceptually, Yes. Nisan's idea is pretty neat and generic. I have not done much survey but some initial reading seems to suggest that it is difficult to give unconditional pseudorandom generators which can fool time bounded complexity classes. May be the instructors can shed more light on this issue.
Thursday, February 19, 2009
Lecture 11
In Lecture 11, we covered:
Telling coke and pepsi apart: Interactive protocol for Graph nonisomorphism;
Interactive proof for Counting-SAT (and so PH is a subset of IP);
The precise power of interaction: IP = PSPACE ;
Perfect completeness and public coins don't change power of IP.
Graded problem set 1 was handed back.
Telling coke and pepsi apart: Interactive protocol for Graph nonisomorphism;
Interactive proof for Counting-SAT (and so PH is a subset of IP);
The precise power of interaction: IP = PSPACE ;
Perfect completeness and public coins don't change power of IP.
Graded problem set 1 was handed back.
Tuesday, February 17, 2009
Lecture 10
Topics covered in Lecture 10:
Barrington's theorem: NC^1 has constant width branching programs (Ben-Or & Cleve's proof which showed width 7)
Lipton-Viglas theorem: SAT can't be solved in simultaneous n^{o(1)} space and n^{1.41} time.
Comments on relativization and limits of diagonalization
Introduction to Interactive proofs
Barrington's theorem: NC^1 has constant width branching programs (Ben-Or & Cleve's proof which showed width 7)
Lipton-Viglas theorem: SAT can't be solved in simultaneous n^{o(1)} space and n^{1.41} time.
Comments on relativization and limits of diagonalization
Introduction to Interactive proofs
Monday, February 16, 2009
Homework 2 -- CORRECTION
A correction has been made to Problem (6c) on the homework. Thanks to Or for pointing out the mistake and giving the correction. The new statement (which is also in the file on the course home page) is:
c) Suppose we form $G'$ by blowing up each node $v$ in $G$ to a clique of size $2nk + w(v)$; we put either all possible edges or no possible edges between the "$u$-clique" and the "$v$-clique", depending on whether or not $(u,v)$ was an edge in $G$. Let $k' = 2nk^2 + r$, where $r \in [2nk]$ is chosen randomly. Show that if $G$'s maximum clique has size $< k$ then with probability $1$, $G'$ has no $k'$-clique; and, if $G$'s maximum clique has size $k$ then $G'$ has a unique $k'$-clique with probability at least $1/(4nk)$.
c) Suppose we form $G'$ by blowing up each node $v$ in $G$ to a clique of size $2nk + w(v)$; we put either all possible edges or no possible edges between the "$u$-clique" and the "$v$-clique", depending on whether or not $(u,v)$ was an edge in $G$. Let $k' = 2nk^2 + r$, where $r \in [2nk]$ is chosen randomly. Show that if $G$'s maximum clique has size $< k$ then with probability $1$, $G'$ has no $k'$-clique; and, if $G$'s maximum clique has size $k$ then $G'$ has a unique $k'$-clique with probability at least $1/(4nk)$.
Solutions to Homework 1
I have just added the solutions to Homework 1 to the course webpage. I am still marking the homeworks, but I hope to return them to you before the end of the week. Thanks for your patience!
UPDATE: I have removed the link to the solutions from the course webpage, but they are still available upon request. If you want a copy, please email me.
UPDATE: I have removed the link to the solutions from the course webpage, but they are still available upon request. If you want a copy, please email me.
Homework 2
Not that I imagine anyone worried about this, but for #4, it's okay to show completeness under poly-time many-one reductions. (I.e., don't bother about log-space reductions.)
Saturday, February 14, 2009
A Quadratic Lower Bound for the Determinant and Permanent Problem
Join me, fellow students, in a quest to discover Complexity-Theory's version of the 'Holy Grail': lower bounds on the size of circuits. This quest began at the 1970s, when the question of $P$ vs. $NP$ first arose. At those early ages, when people were naive, optimistic, and still new to the question $P \stackrel {?} {=} NP$, they sought to separate $NP$ from $P$. One direction, that initially seemed promising, was though circuit size. Clearly, $P \subset P/poly$. Furthermore, Karp showed that many functions belong to $NP$, and we know many functions with super-polynomial circuit-complexity do exist. So the hope was one would be able to show that some function in $NP$ must have large circuit-size, thus proving $P \neq NP$. In fact, one can show super-polynomial lower bound for some function in any level of the $PH$, and that will prove such a separation. And since Toda's theorem gives, $PH \subset P^{#P}$, the hope was that the Permanent, a $#P$-complete function, will have super-polynomial large circuits.
Recall that the Permanent is a function of numbers: $Perm = \sum_{\sigma \in S_n} \Pi_{i} M_{i, \sigma(i)}$, whereas circuits were defined over boolean values. So we introduce arithmetics circuits. Arithmetic circuits have $\oplus, \otimes$ gates (with fan-in 2), and $\ominus$ gates (with fan-in 1), representing the arithmetic $+, \times, -$ operations over some field $F$, and additionally uses constants in $F$. Clearly, every polynomial (and in particular the Permanent and the Determinant) can be represented as an arithmetic circuit, and furthermore, one can reduce any boolean circuit to an arithmetic circuit (representing NOT as $1 \ominus x$ and AND as $x\otimes y$). Using arithmetic circuits, Valiant defined in 1979 the arithmetics analogs of $P$ and $NP$:
Definition 1: A polynomial $p(\bar x)$ of degree $n^{O(1)}$ is in $VP$ if there exists a arithmetic circuit family of size $n^{O(1)}$ that computes it.
Definition 2: A polynomial $p(\bar x)$ of degree $n^{O(1)}$ is in $VNP$ if for some $m$ (polynomially bounded in $n$) there exists a family of polynomials $q_{n+m} \in VP$ s.t. $p(\bar x) = \sum_{\bar y \in \{0,1\}^m} q(\bar x, \bar y)$. For such $p$ and $q$, we say that $p$ is a projection of $q$.
Valiant showed that any polynomial in $VNP$ is a projection of the Permanent. He also showed a nice characterization of the functions of $VP$, which will take us back to linear algebra. Recall that an affine transformation of vector spaces is a combination of a linear transformation and a translation. We look at affine functions from the vector space $F[x_1, x_2, \ldots, x_d]$ of polynomials in $d$ variables over $F$, to the vector space $M_n(F)$ of all $n\times n$ matrices.
Definition 3: We say that a polynomial $p\in F[x_1, \ldots, x_d]$ has determinant complexity $n$ if any affine mapping $f:F[x_1, \ldots, x_d] \rightarrow M_n(F)$ s.t. $p \equiv \det\circ f$, must map $F[x_1, \ldots, x_d]$ to matrices of size $n\times n$ (or larger).
Valiant showed that if $p$ has circuit complexity $c$, then its determinant complexity is $\leq 2c$, so all functions in $VP$ have polynomially bounded determinant complexity. Hence, in order to separate $VNP$ from $VP$, one aspires to show that the determinant complexity of the Permanent is super-polynomial. Alas, until 2004, the best determinant-complexity lower bounds were linear in $n$. In 2004, Mignon and Ressayre showed a quadratic lower bound:
Theorem: If the characteristic of $F$ is $0$, then the determinant-complexity of the Permanent is at least $n^2/2$.
The proof of this theorem naturally involves some linear algebra, and requires the definition of a special linear operator. If $f:V\rightarrow F$ is a differentiable function, then we can define the tangent map $Tf: V\rightarrow V^*$, by: $Tf(v) = \langle \frac {\partial f}{\partial x_i}(v), \cdot \rangle$. I.e., we map every $v\in V$ to a linear functional $T_vf$, where $T_vf(w)$ is the scalar product of $\nabla f(v)$ and $w$. Using the tangent and the fact that the space of linear functionals is a vector space, we can now define a tangent to the tangent. Let $T^2f: V \rightarrow \textrm{Hom}(V, V^*)$ be defined by $T^2f(v) = (\cdot)^TH_f(v)(\cdot)$, where $H_f(v) = \left(\frac {\partial^2 f}{\partial x_i \partial x_j}(v)\right)_{i,j=1}$. I.e., we map every $v\in V$ to a bilinear function $A_v(\cdot, \cdot)$ where $A_v$ is constructed by the 2nd order partial derivatives of $f$ at $v$. Alternatively, one can think of $f(v)$ as a map $T_{v}^2f:V\rightarrow V^*$, where $(T_{v}^2f)(w)$ is the linear functional $\langle A_v w, \cdot\rangle$. Recall that any bilinear function (and in particular $A_v$) has a rank, which is the rank of the matrix.
Here is the proof of Mignon and Ressayre's theorem in a nutshell. Let $f:M_n(F)\rightarrow M_m(F)$ be an affine function s.t. $Perm_n = \det_m\circ f$. Then the following 3 claims hold:
Claim 1. $Perm_n$ is isomorphic to restricting $\det_m$ to the image of $f$, i.e. $Perm_n \simeq g$ where $g = \det_m |_{\textrm{Im}(f)}$. Since $g$ is a restriction of $\det_m$, we get $\textrm{rank}(T_{A}^{2} g) \leq \textrm{rank}(T_{A}^{2}\det_m)$.
Claim 2. There exists some non-invertible $A\in M_n(F)$, s.t. $T_{A}^{2} Perm_n$ has rank $= n^2$. (This is the most non-trivial part.)
Claim 3. For any non-invertible matrix $A$ it must hold that $\textrm{rank}(T_{A}^{2} \det_m) \leq 2m$.
Combining the 3 steps together, we deduce the inequalities $n^2 = \textrm{rank}(T_{A}^2Perm_n) = \textrm{rank}(T_A^2 g) \leq \textrm{rank}(T_A^2\det\_m) \leq 2m$
None of the proofs of 1,2 or 3 is hard, and they all boil down to looking at the matrix generated by the $T^2$ operator. If
is our variable matrix, then we denote $P = Perm_n(X)$. For the minor $X_{i,j}$ (removing the $i$th row and the $j$th column of $X$), we denote $P_{i,j} = Perm_{n-1}(X_{i,j})$. For any $i\neq i', j\neq j'$, we denote $X_{\{i,i'\},\{j,j'\}}$ to be the minor of $X$ we get by removing both $i$ and $i'$ rows, and $j$ and $j'$ columns, and denote $P_{\{i,i'\},\{j,j'\}} = Perm_{n-2}(X_{\{i,i'\},\{j,j'\}})$. Then observe the following: $T^{2}Perm_n$ is the $n^2\times n^2$ matrix 
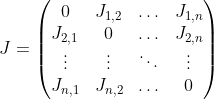where for every $i \neq i'$, we have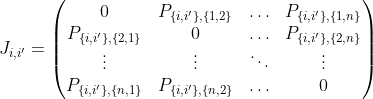 
Proving Claim 2 is the result of looking at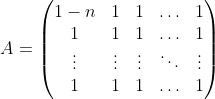
. By sheer computation, they show that $T_A^{2}Perm_n$ is of the form 
, for two particular, invertible, $B$ and $C$, and show that this gives a $n^2 \times n^2$-matrix of full rank. We comment that the elements of $B$ and $C$ are multiplications of large factorials, so $B$ and $C$ are invertible because of the zero characteristic of $F$.
Proving Claim 3 uses a similar observation, based on the structure of $T^2$. If $X$ is a non-invertible matrix, then by changing basis, $X$ can be turned into $X'$, which is a diagonal matrix with some 0 entries on the main diagonal. $T_X^2\det$ and $T_{X'}^2\det$ will have the same rank. If we replace $Perm$ in $\det$, we get that $T_{X'}^2\det$ has the exact same structure as it had for the Permanent (replacing $P_{\{i,i'\},\{j,j'\}}$ with $D_{\{i,i'\},\{j,j'\}}$, the determinant of the same minor). However, since $X'$ is diagonal and non-invertible, then the determinant is $0$ for almost everywhere.
Proving Claim 1 boils down to showing the $f$ is injective, thus isomorphic over its image. If $f$ isn't injective, then exists a non-zero $v \in \textrm{Ker}(f)$. Hence, $\forall x, \forall \lambda \in F$ it holds that $Perm_n(x+\lambda v) = \det_m(f(x)+\lambda f(v)) = Perm_n(x)$, so the gradient of $Perm_n$ at $v$ must be $0$. Alternatively, every $T_xPerm_n$ maps $v$ into the $0$-functional. So for every $y$ it holds that $T_y^2Perm_n$ is a bilinear mapping, that maps every $x$ into a functional $\phi_x$ which is $0$ over $v$. Thus for every $y$ it holds that $T_y^2Perm_n$ is not of full rank. In particular, $T_A^2Perm_n$ has of rank strictly smaller than $n^2$, which contradicts Claim 2. The proof of the theorem is done.
SPOILER ALERT: The quest for lower bounds on circuits is (thus far) unsuccessful. Obviously, we still don't know how to show super-polynomial lower bounds on the determinant complexity of the Permanent. To this day, lower bounds are known only to a very restricted class of circuits (such as $AC^0$ or monotone circuits). In fact, Razborov and Rudich showed in 1995 that proving lower bounds using the currently known techniques is intrinsically difficult. However, there is some positive sign: in 2004, Kabanets and Impagliazzo showed that under the assumption $coRP = P$, either the Permanent or some function in $NEXP$ doesn't have polynomial-size circuits.
Recall that the Permanent is a function of numbers: $Perm = \sum_{\sigma \in S_n} \Pi_{i} M_{i, \sigma(i)}$, whereas circuits were defined over boolean values. So we introduce arithmetics circuits. Arithmetic circuits have $\oplus, \otimes$ gates (with fan-in 2), and $\ominus$ gates (with fan-in 1), representing the arithmetic $+, \times, -$ operations over some field $F$, and additionally uses constants in $F$. Clearly, every polynomial (and in particular the Permanent and the Determinant) can be represented as an arithmetic circuit, and furthermore, one can reduce any boolean circuit to an arithmetic circuit (representing NOT as $1 \ominus x$ and AND as $x\otimes y$). Using arithmetic circuits, Valiant defined in 1979 the arithmetics analogs of $P$ and $NP$:
Definition 1: A polynomial $p(\bar x)$ of degree $n^{O(1)}$ is in $VP$ if there exists a arithmetic circuit family of size $n^{O(1)}$ that computes it.
Definition 2: A polynomial $p(\bar x)$ of degree $n^{O(1)}$ is in $VNP$ if for some $m$ (polynomially bounded in $n$) there exists a family of polynomials $q_{n+m} \in VP$ s.t. $p(\bar x) = \sum_{\bar y \in \{0,1\}^m} q(\bar x, \bar y)$. For such $p$ and $q$, we say that $p$ is a projection of $q$.
Valiant showed that any polynomial in $VNP$ is a projection of the Permanent. He also showed a nice characterization of the functions of $VP$, which will take us back to linear algebra. Recall that an affine transformation of vector spaces is a combination of a linear transformation and a translation. We look at affine functions from the vector space $F[x_1, x_2, \ldots, x_d]$ of polynomials in $d$ variables over $F$, to the vector space $M_n(F)$ of all $n\times n$ matrices.
Definition 3: We say that a polynomial $p\in F[x_1, \ldots, x_d]$ has determinant complexity $n$ if any affine mapping $f:F[x_1, \ldots, x_d] \rightarrow M_n(F)$ s.t. $p \equiv \det\circ f$, must map $F[x_1, \ldots, x_d]$ to matrices of size $n\times n$ (or larger).
Valiant showed that if $p$ has circuit complexity $c$, then its determinant complexity is $\leq 2c$, so all functions in $VP$ have polynomially bounded determinant complexity. Hence, in order to separate $VNP$ from $VP$, one aspires to show that the determinant complexity of the Permanent is super-polynomial. Alas, until 2004, the best determinant-complexity lower bounds were linear in $n$. In 2004, Mignon and Ressayre showed a quadratic lower bound:
Theorem: If the characteristic of $F$ is $0$, then the determinant-complexity of the Permanent is at least $n^2/2$.
The proof of this theorem naturally involves some linear algebra, and requires the definition of a special linear operator. If $f:V\rightarrow F$ is a differentiable function, then we can define the tangent map $Tf: V\rightarrow V^*$, by: $Tf(v) = \langle \frac {\partial f}{\partial x_i}(v), \cdot \rangle$. I.e., we map every $v\in V$ to a linear functional $T_vf$, where $T_vf(w)$ is the scalar product of $\nabla f(v)$ and $w$. Using the tangent and the fact that the space of linear functionals is a vector space, we can now define a tangent to the tangent. Let $T^2f: V \rightarrow \textrm{Hom}(V, V^*)$ be defined by $T^2f(v) = (\cdot)^TH_f(v)(\cdot)$, where $H_f(v) = \left(\frac {\partial^2 f}{\partial x_i \partial x_j}(v)\right)_{i,j=1}$. I.e., we map every $v\in V$ to a bilinear function $A_v(\cdot, \cdot)$ where $A_v$ is constructed by the 2nd order partial derivatives of $f$ at $v$. Alternatively, one can think of $f(v)$ as a map $T_{v}^2f:V\rightarrow V^*$, where $(T_{v}^2f)(w)$ is the linear functional $\langle A_v w, \cdot\rangle$. Recall that any bilinear function (and in particular $A_v$) has a rank, which is the rank of the matrix.
Here is the proof of Mignon and Ressayre's theorem in a nutshell. Let $f:M_n(F)\rightarrow M_m(F)$ be an affine function s.t. $Perm_n = \det_m\circ f$. Then the following 3 claims hold:
Claim 1. $Perm_n$ is isomorphic to restricting $\det_m$ to the image of $f$, i.e. $Perm_n \simeq g$ where $g = \det_m |_{\textrm{Im}(f)}$. Since $g$ is a restriction of $\det_m$, we get $\textrm{rank}(T_{A}^{2} g) \leq \textrm{rank}(T_{A}^{2}\det_m)$.
Claim 2. There exists some non-invertible $A\in M_n(F)$, s.t. $T_{A}^{2} Perm_n$ has rank $= n^2$. (This is the most non-trivial part.)
Claim 3. For any non-invertible matrix $A$ it must hold that $\textrm{rank}(T_{A}^{2} \det_m) \leq 2m$.
Combining the 3 steps together, we deduce the inequalities $n^2 = \textrm{rank}(T_{A}^2Perm_n) = \textrm{rank}(T_A^2 g) \leq \textrm{rank}(T_A^2\det\_m) \leq 2m$
None of the proofs of 1,2 or 3 is hard, and they all boil down to looking at the matrix generated by the $T^2$ operator. If
Proving Claim 2 is the result of looking at
Proving Claim 3 uses a similar observation, based on the structure of $T^2$. If $X$ is a non-invertible matrix, then by changing basis, $X$ can be turned into $X'$, which is a diagonal matrix with some 0 entries on the main diagonal. $T_X^2\det$ and $T_{X'}^2\det$ will have the same rank. If we replace $Perm$ in $\det$, we get that $T_{X'}^2\det$ has the exact same structure as it had for the Permanent (replacing $P_{\{i,i'\},\{j,j'\}}$ with $D_{\{i,i'\},\{j,j'\}}$, the determinant of the same minor). However, since $X'$ is diagonal and non-invertible, then the determinant is $0$ for almost everywhere.
Proving Claim 1 boils down to showing the $f$ is injective, thus isomorphic over its image. If $f$ isn't injective, then exists a non-zero $v \in \textrm{Ker}(f)$. Hence, $\forall x, \forall \lambda \in F$ it holds that $Perm_n(x+\lambda v) = \det_m(f(x)+\lambda f(v)) = Perm_n(x)$, so the gradient of $Perm_n$ at $v$ must be $0$. Alternatively, every $T_xPerm_n$ maps $v$ into the $0$-functional. So for every $y$ it holds that $T_y^2Perm_n$ is a bilinear mapping, that maps every $x$ into a functional $\phi_x$ which is $0$ over $v$. Thus for every $y$ it holds that $T_y^2Perm_n$ is not of full rank. In particular, $T_A^2Perm_n$ has of rank strictly smaller than $n^2$, which contradicts Claim 2. The proof of the theorem is done.
SPOILER ALERT: The quest for lower bounds on circuits is (thus far) unsuccessful. Obviously, we still don't know how to show super-polynomial lower bounds on the determinant complexity of the Permanent. To this day, lower bounds are known only to a very restricted class of circuits (such as $AC^0$ or monotone circuits). In fact, Razborov and Rudich showed in 1995 that proving lower bounds using the currently known techniques is intrinsically difficult. However, there is some positive sign: in 2004, Kabanets and Impagliazzo showed that under the assumption $coRP = P$, either the Permanent or some function in $NEXP$ doesn't have polynomial-size circuits.
Friday, February 13, 2009
Combinatorial Complexity
There is a certain broad area of complexity theory which does not have a proper name.
As far as it occurs to me at this instant, there are (at least) three big areas of complexity theory:
1. "Structural complexity theory". This refers to understanding the relationships between complexity classes, bounding and classifying time vs. space vs. randomness, understanding reductions, etc.
2. "Algorithmic complexity theory". I just made this name up, but I'm thinking here about the area of understanding the complexity of various specific problems; I think of proving NP-hardness results as falling into this area, so I would put inapproximability and PCPs into this category.
3. The mystery area I referred to at the beginning of this post. I guess my best attempt at naming this category would be either "Combinatorial complexity", or "Lower bounds". Here I mean the study of things like formula size/depth, constant-depth circuit size, branching program sizes, decision tree size, DNF size... roughly, the study of non-uniform classes of computation that are "small" enough that one can make reasonable progress on proving lower bounds.
The impetus for this post is to point you to a nice-looking graduate course on this 3rd area being taught by Rocco Servedio at Columbia this term. If the lecture notes continue, this should be a great resource for this huge area of complexity theory.
As far as it occurs to me at this instant, there are (at least) three big areas of complexity theory:
1. "Structural complexity theory". This refers to understanding the relationships between complexity classes, bounding and classifying time vs. space vs. randomness, understanding reductions, etc.
2. "Algorithmic complexity theory". I just made this name up, but I'm thinking here about the area of understanding the complexity of various specific problems; I think of proving NP-hardness results as falling into this area, so I would put inapproximability and PCPs into this category.
3. The mystery area I referred to at the beginning of this post. I guess my best attempt at naming this category would be either "Combinatorial complexity", or "Lower bounds". Here I mean the study of things like formula size/depth, constant-depth circuit size, branching program sizes, decision tree size, DNF size... roughly, the study of non-uniform classes of computation that are "small" enough that one can make reasonable progress on proving lower bounds.
The impetus for this post is to point you to a nice-looking graduate course on this 3rd area being taught by Rocco Servedio at Columbia this term. If the lecture notes continue, this should be a great resource for this huge area of complexity theory.
Thursday, February 12, 2009
Lecture 9
Topics covered in Lecture 9:
Randomized space: $RL \subseteq BPL \subseteq L^{3/2}$ (Saks-Zhou Theorem), USTCON $\in RL$. Circuits (as parallel computation): $NC$ vs. $P$, $NC^0$, $NC^1 \subseteq L \subseteq NL \subseteq NC^2$, matrix multiplication in $NC^1$, nonuniform $NC^1 = $ poly-size formulas. Branching programs: non-uniform $L = $ poly-size branching programs, small-width branching programs, statement of Barrington's Theorem (nonuniform $NC^1 = $ constant-width poly-size branching programs).
Randomized space: $RL \subseteq BPL \subseteq L^{3/2}$ (Saks-Zhou Theorem), USTCON $\in RL$. Circuits (as parallel computation): $NC$ vs. $P$, $NC^0$, $NC^1 \subseteq L \subseteq NL \subseteq NC^2$, matrix multiplication in $NC^1$, nonuniform $NC^1 = $ poly-size formulas. Branching programs: non-uniform $L = $ poly-size branching programs, small-width branching programs, statement of Barrington's Theorem (nonuniform $NC^1 = $ constant-width poly-size branching programs).
Tuesday, February 10, 2009
Office hours today
Just a reminder that while class is canceled today, I will still be holding my office hours between 12:30pm and 1:30pm today, in Wean 3709.
Monday, February 9, 2009
Friday, February 6, 2009
Average Case Hardness
In 1971, Stephen Cook showed that the boolean satisfiability problem is NP-Complete under polynomial time reductions. Soon afterward, Karp showed that many natural combinatorial problems (Vertex Cover, Clique, Hamiltonian Circuit etc..) were also NP-Complete. However, these results are often misinterpreted. Because most computer scientists believe $P \neq NP$ it is easy to assume that it is always hard to solve $3-SAT$. This is not true. In fact most randomly generated $3-SAT$ instances can be solved efficiently by algorithms like DPLL. Assuming that $P \neq NP$ then all we may conclude is that there is no efficient algorithm to solve these problems in the worst case. It is conceivable that $NP-Complete$ problems could still admit polynomial time algorithms for average instances.
Notice that problems which are not hard on average are poor candidates for cryptography and one-way functions. Protocols such as Diffie-Hellman would absolutely fail if it was easy to compute the discrete logarithm (given a multiplicative generator $g$ in a finite field mod p, and an integer $x$ compute $a$ such that $g^a \equiv x$ mod p) for average instances. Russel Impagliazzo (A Personal View of Average-Case Complexity) describes several possible worlds and their applications to cryptography.
World 1: Algorithmica $P = NP$ or $NP \subseteq BPP$. We all know that such a result would revolutionize computer science and machine learning. However, cryptography would be impossible in this world.
World 2: Heuristica $P \neq NP$, but, over any efficiently computable distribution, $NP-Complete$ problems are tractable on average. Intuitively, there are hard instances of $NP$ problems, but the problem of finding hard instances is itself intractable. Once again, crytography would most likely not be feasible in Heuristica because eavesdroppers could solve problems in a time comparable to the time it took to generate the problem.
World 3: Pessiland $P\neq NP$ AND there are problems which are hard in the average-case for efficiently computable distribution. However, there are no one way functions. This means that given $f(x)$ it is usually possible to find some $x'$ such that $f(x') = f(x)$ in time comparable to the ammount of time needed to compute $f(x)$. In Pessiland, it would be easy to generate hard instances of $NP$ problems, but there would be no way of generating hard (presolved) instances of $NP$ problems. Public key crytography would still not be possible. Thus, Average Case Hardness is a necessary (but not sufficient) condition for cryptography.
Worlds 4 and 5: Minicrypt and Cryptomania. In Cryptomania, almost any cryptographic task is possible. This is the world we typically assume we live in, because we assume protocols like RSA and Diffie-Hellman are secure. However, the only evidence that the Discrete Logarithm problem is hard is that fact that we don't know of an efficient algorithm to compute it. In reality, there is no theoretical reason why the problem should be hard. In fact, Peter Shor recently showed that Discrete Logarithms can be solved efficiently on a Quantum Computer.
Fortunately for cryptographers, the Discrete Logarithm problem is a beautiful example of self reducibility.
Lemma: Suppose that we had an algorithm $A$ which computes the the discrete logarithm efficiently (in time $poly(n)$, $n = \log p$) for at least $\frac{p}{poly(n)}$ values of $x$, then there is an efficient ZPP algorithm $A'$ to compute the discrete logarithm efficiently.
Proof (Sketch): We can pick $k$ such that $A$ solves at least $\frac{p}{n^k}$ instances in time $O(n^k)$, let $m = n^{2k}$.
Input: Generator g, Integer x, Prime p
Output: $a$ such that $g^a \equiv x$ mod p or FAIL
For $i = 1...m$
---$a_i \leftarrow Unif(0,p-2)$
--- $x_i = g^{a_i}$ mod p
---// Number Theory Fact: this is equivalent to picking $x_i\leftarrow Unif(1,...,p-2)$
---If $A(g,x\times x_i,p)$ returns $a'$ in $n^k$ steps then
------// Now we know the answer due to number theory:
------// $x \times x_i \equiv g^{a_i} g^{a}$ mod p
------// $ g^{a_i} g^{a} = g^{a_i + a} \equiv g^{a'} $ mod p
------// $a = a' - a_i$
------return $a = a' - a_i$
Output Failed
It is not too hard to verify that the algorithm takes polynomial time and with high probability computes the correct answer. QED
I am unaware of any NP-Complete problems which are self reducible in a similar sense as the Discrete Logarithm problem. If such a self reduction was found I suspect that this would be a very interesting result in complexity theory.
A more common approach to the problem of defining average case hardness is that of Leonid Levin. Levin (Average Case Complete Problems) defines the notion of a random NP problem and a complete random NP problem. His definitions are tedious and hard to follow at times, but they are worth the time and energy to understand.
Definition: A random problem is a pair $(\mu, R)$ where $R \subset \mathbb{N}^2$ is an instance witness and $\mu: \mathbb{N} \rightarrow [0,1]$ is a probability distribution function.
A problem instance is an integer $x$ is the problem instance. $x \in L$ if and only if there is $y$ such that $(x,y) \in R$. The a probability distribution function $\mu(x)$ gives the probability of all problem instances which do not exceed $x$.
Notation: $\mu'(x) = \mu(x)-\mu(x-1)$ is the probability density function.
Also, by convention
Definition: A random problem is in NP if both $R$ and $\mu$ are both computable in polynomial time. We call such a problem a random NP Problem.
In other words, given a tuple $(x,y)$ (a problem instance and a verifier) we can decide whether or not $(x,y) \in R$ in polynomial time in $|x|$. We can also sample from the distribution $\mu$ in polynomial time.
Definition: A random problem $(\mu, R)$ is polynomial on average if there is a Turing Machine $M$, which runs in time $t(x)^k$ such that:
The first condition guarantees that $M$ actually decides the problem. The second condition guarantees that the Turing Machine must run quickly on average instances sampled from our distribution $\mu$.
Definition: We say that the probability distribution function $\mu_1$ dominates $\mu$ if $\exists k \forall x \frac{\mu'(x)}{\mu_1(x)} \leq |x|^k$. In such a case we write $\mu \prec \mu_1$.
Intuitively, this definition guarantees that all of the 'likely' instances of $\mu$ are also the 'likely' inputs of $\mu_1$
We are finally ready to define the notion of reduction between random NP problems.
Definition:A polynomial time computable function $f$ reduces a random NP problem $(\mu_1, R_1)$ to another random NP problem $(f(\mu_2), R_2)$ if the following conditions hold:
Levin shows that these reductions are closed under composition. If $A(x)$ is an algorithm that is fast on average for $(f(\mu_2), R_2)$ then $A(f(x))$ runs at most polynomially slower for $(\mu_1, R_1)$.
Definition: A random NP problem is complete if every random NP problem is reducible to it.
Levin proved that Tiling is an NP-complete random problem. Other natural combinatorial problems such as Graph Coloring and Matrix Decomposition have also been shown to be NP-complete random problems.
Notice that problems which are not hard on average are poor candidates for cryptography and one-way functions. Protocols such as Diffie-Hellman would absolutely fail if it was easy to compute the discrete logarithm (given a multiplicative generator $g$ in a finite field mod p, and an integer $x$ compute $a$ such that $g^a \equiv x$ mod p) for average instances. Russel Impagliazzo (A Personal View of Average-Case Complexity) describes several possible worlds and their applications to cryptography.
World 1: Algorithmica $P = NP$ or $NP \subseteq BPP$. We all know that such a result would revolutionize computer science and machine learning. However, cryptography would be impossible in this world.
World 2: Heuristica $P \neq NP$, but, over any efficiently computable distribution, $NP-Complete$ problems are tractable on average. Intuitively, there are hard instances of $NP$ problems, but the problem of finding hard instances is itself intractable. Once again, crytography would most likely not be feasible in Heuristica because eavesdroppers could solve problems in a time comparable to the time it took to generate the problem.
World 3: Pessiland $P\neq NP$ AND there are problems which are hard in the average-case for efficiently computable distribution. However, there are no one way functions. This means that given $f(x)$ it is usually possible to find some $x'$ such that $f(x') = f(x)$ in time comparable to the ammount of time needed to compute $f(x)$. In Pessiland, it would be easy to generate hard instances of $NP$ problems, but there would be no way of generating hard (presolved) instances of $NP$ problems. Public key crytography would still not be possible. Thus, Average Case Hardness is a necessary (but not sufficient) condition for cryptography.
Worlds 4 and 5: Minicrypt and Cryptomania. In Cryptomania, almost any cryptographic task is possible. This is the world we typically assume we live in, because we assume protocols like RSA and Diffie-Hellman are secure. However, the only evidence that the Discrete Logarithm problem is hard is that fact that we don't know of an efficient algorithm to compute it. In reality, there is no theoretical reason why the problem should be hard. In fact, Peter Shor recently showed that Discrete Logarithms can be solved efficiently on a Quantum Computer.
Fortunately for cryptographers, the Discrete Logarithm problem is a beautiful example of self reducibility.
Lemma: Suppose that we had an algorithm $A$ which computes the the discrete logarithm efficiently (in time $poly(n)$, $n = \log p$) for at least $\frac{p}{poly(n)}$ values of $x$, then there is an efficient ZPP algorithm $A'$ to compute the discrete logarithm efficiently.
Proof (Sketch): We can pick $k$ such that $A$ solves at least $\frac{p}{n^k}$ instances in time $O(n^k)$, let $m = n^{2k}$.
Input: Generator g, Integer x, Prime p
Output: $a$ such that $g^a \equiv x$ mod p or FAIL
For $i = 1...m$
---$a_i \leftarrow Unif(0,p-2)$
--- $x_i = g^{a_i}$ mod p
---// Number Theory Fact: this is equivalent to picking $x_i\leftarrow Unif(1,...,p-2)$
---If $A(g,x\times x_i,p)$ returns $a'$ in $n^k$ steps then
------// Now we know the answer due to number theory:
------// $x \times x_i \equiv g^{a_i} g^{a}$ mod p
------// $ g^{a_i} g^{a} = g^{a_i + a} \equiv g^{a'} $ mod p
------// $a = a' - a_i$
------return $a = a' - a_i$
Output Failed
It is not too hard to verify that the algorithm takes polynomial time and with high probability computes the correct answer. QED
I am unaware of any NP-Complete problems which are self reducible in a similar sense as the Discrete Logarithm problem. If such a self reduction was found I suspect that this would be a very interesting result in complexity theory.
A more common approach to the problem of defining average case hardness is that of Leonid Levin. Levin (Average Case Complete Problems) defines the notion of a random NP problem and a complete random NP problem. His definitions are tedious and hard to follow at times, but they are worth the time and energy to understand.
Definition: A random problem is a pair $(\mu, R)$ where $R \subset \mathbb{N}^2$ is an instance witness and $\mu: \mathbb{N} \rightarrow [0,1]$ is a probability distribution function.
A problem instance is an integer $x$ is the problem instance. $x \in L$ if and only if there is $y$ such that $(x,y) \in R$. The a probability distribution function $\mu(x)$ gives the probability of all problem instances which do not exceed $x$.
Notation: $\mu'(x) = \mu(x)-\mu(x-1)$ is the probability density function.
Also, by convention
- $|x| = \lceil \log x \rceil$
- $R(x,y)$ is true if and only if $(x,y) \in R$.
Definition: A random problem is in NP if both $R$ and $\mu$ are both computable in polynomial time. We call such a problem a random NP Problem.
In other words, given a tuple $(x,y)$ (a problem instance and a verifier) we can decide whether or not $(x,y) \in R$ in polynomial time in $|x|$. We can also sample from the distribution $\mu$ in polynomial time.
Definition: A random problem $(\mu, R)$ is polynomial on average if there is a Turing Machine $M$, which runs in time $t(x)^k$ such that:
- $M(x) \leftrightarrow \exists y R(x,y)$
- $\Sigma_{x=1}^\infty \mu'(x) \frac{t(x)}{|x|}$ converges.
The first condition guarantees that $M$ actually decides the problem. The second condition guarantees that the Turing Machine must run quickly on average instances sampled from our distribution $\mu$.
Definition: We say that the probability distribution function $\mu_1$ dominates $\mu$ if $\exists k \forall x \frac{\mu'(x)}{\mu_1(x)} \leq |x|^k$. In such a case we write $\mu \prec \mu_1$.
Intuitively, this definition guarantees that all of the 'likely' instances of $\mu$ are also the 'likely' inputs of $\mu_1$
We are finally ready to define the notion of reduction between random NP problems.
Definition:A polynomial time computable function $f$ reduces a random NP problem $(\mu_1, R_1)$ to another random NP problem $(f(\mu_2), R_2)$ if the following conditions hold:
- $f(\mu_2)(x) = \Sigma_{f(y) \leq x} \mu'(y)$
- $\mu_1 \prec \mu_2$
- $\exists y_1 R(x,y_1) \leftrightarrow \exists y_2 R(f(x),y_2)$
Levin shows that these reductions are closed under composition. If $A(x)$ is an algorithm that is fast on average for $(f(\mu_2), R_2)$ then $A(f(x))$ runs at most polynomially slower for $(\mu_1, R_1)$.
Definition: A random NP problem is complete if every random NP problem is reducible to it.
Levin proved that Tiling is an NP-complete random problem. Other natural combinatorial problems such as Graph Coloring and Matrix Decomposition have also been shown to be NP-complete random problems.
Thursday, February 5, 2009
Lecture 8
Today we proved the following five theorems:
1. $NSPACE(s(n)) \subseteq DTIME(2^{O(s(n))}).
2. ST-Connectivity is $NL$-complete.
3. Savitch's Theorem: $NSPACE(s(n)) \subseteq DSPACE(s(n)^2)$.
4. TQBF is $PSPACE$-complete.
5. Immerman-Szelepcsényi Theorem: $NSPACE(s(n)) \subseteq coNSPACE(s(n))$.
Here $s(n) \geq \log n$ is a space-constructible bound. (I believe that for most of these, if you want to get really really technical, you can even drop space-constructibility :)
1. $NSPACE(s(n)) \subseteq DTIME(2^{O(s(n))}).
2. ST-Connectivity is $NL$-complete.
3. Savitch's Theorem: $NSPACE(s(n)) \subseteq DSPACE(s(n)^2)$.
4. TQBF is $PSPACE$-complete.
5. Immerman-Szelepcsényi Theorem: $NSPACE(s(n)) \subseteq coNSPACE(s(n))$.
Here $s(n) \geq \log n$ is a space-constructible bound. (I believe that for most of these, if you want to get really really technical, you can even drop space-constructibility :)
Tuesday, February 3, 2009
Lecture 7
Today we covered: Permanent is #P-complete (statement); Toda's Theorem; statements of basic space theorems (non-deterministic space $s$ in deterministic $2^{O(s)}$ time, Savitch's Theorem, Immerman-Szelepcsenyi Theorem).
Monday, February 2, 2009
Homework 2
Homework 2 has been posted slightly early for your enjoyment! It's linked to on the course home page. Due Feb. 17.
I assume you all saw the hints for Homework 1 in the comments to the previous post.
I assume you all saw the hints for Homework 1 in the comments to the previous post.
Subscribe to:
Posts (Atom)
Posts
